Opgave 1

Op de Nederlandse woningmarkt voor sociale huurwoningen grijpt de overheid in met een maximumprijs van € 700 huur per maand.
Op die manier hoopt de overheid deze eenvoudige woningen betaalbaar te houden voor mensen met een laag inkomen.

Deze markt kan modelmatig als volgt worden weergegeven:

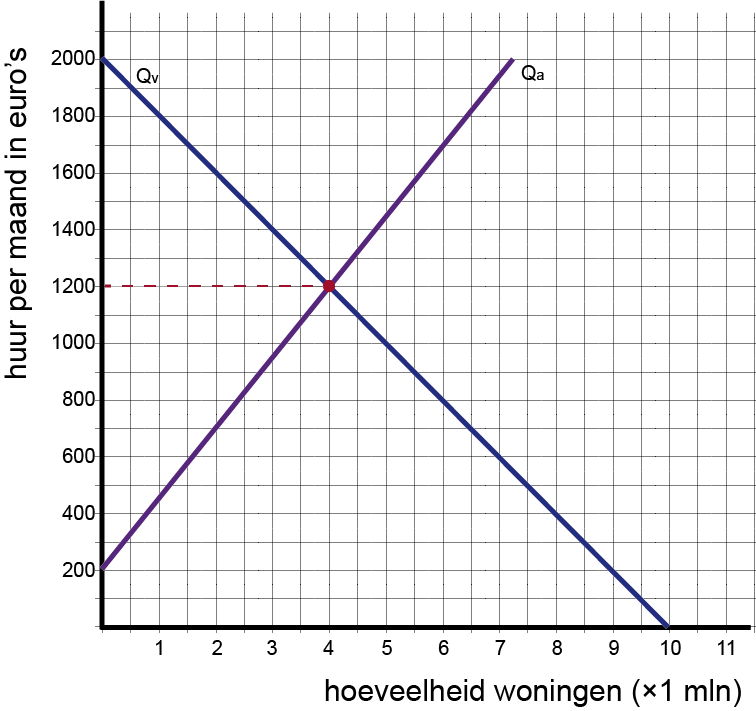
Qv = -0,005P + 10
Qa = 0,004P – 0,8

waarbij:
P = huur per maand in euro’s
Q = hoeveelheid woningen × mln.

1 Teken de vraag- en aanbodlijn in één grafiek.
(neem horizontaal 1 cm = 1 mln woningen ; verticaal 1 cm = 200 euro)
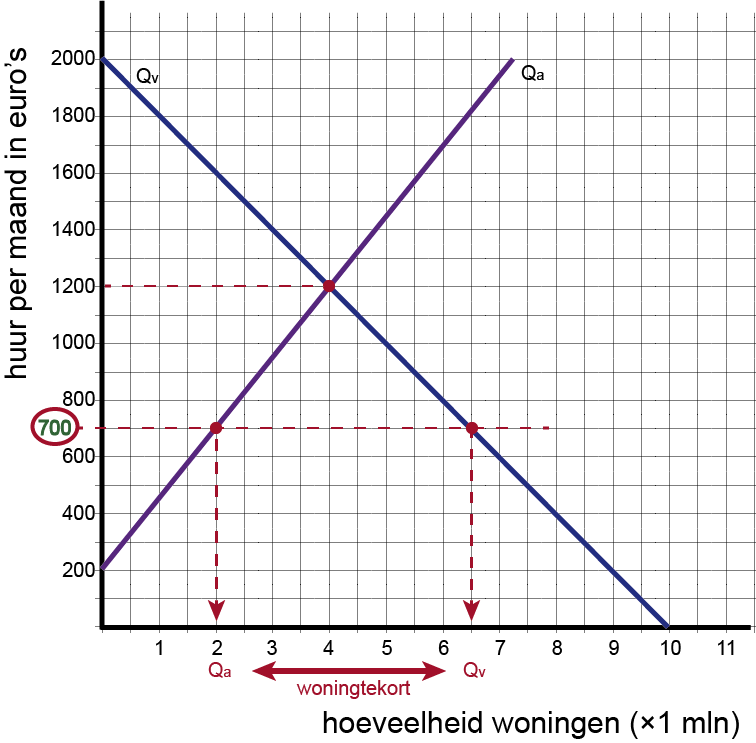
2 Ontstaat er een tekort of een overschot aan woningen? Verklaar je antwoord met een berekening.
3 Geef dit overschot/tekort duidelijk aan in de grafiek van vraag 1.
4 Wat kan de overheid aan dit (vraag 2 en 3) probleem doen?
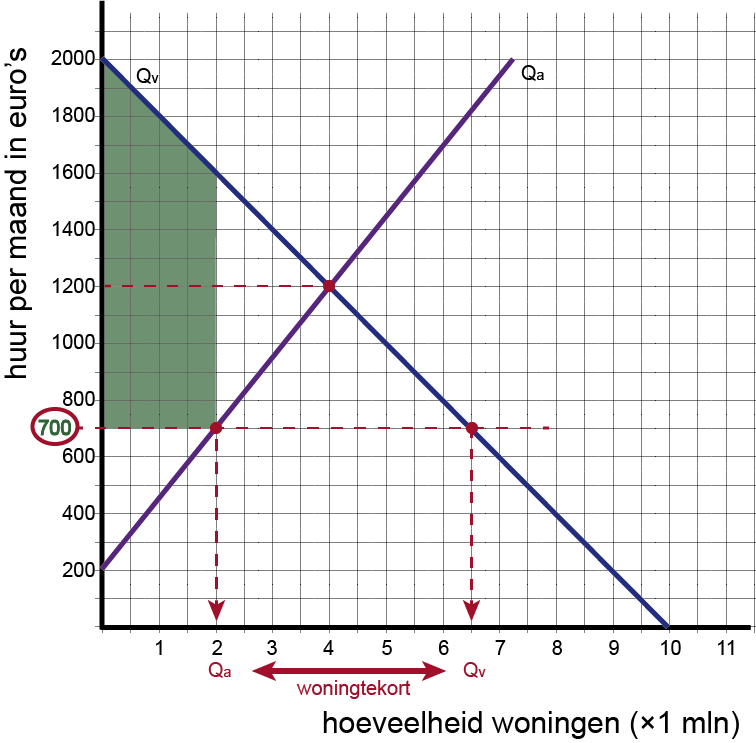
5 Arceer het consumentensurplus.

Opgave 1

1

maximumprijs2_00
2

Bij een huur van € 700 per maand zal:

DE VRAAG:

Qv = -0,005P + 10
Qv = -0,005×700 + 10
Qv = 6,5

HET AANBOD:

Qa = 0,004P – 0,8
Qa = 0,004×700 – 0,8
Qa = 2

Er worden dus 6,5 miljoen woningen gevraagd, maar slechts 2 miljoen aangeboden.
Er ontstaat dus een tekort aan woningen van 4,5 mln.
3

maximumprijs2_01
4

Op korte termijn moet de overheid een systeem verzinnen om de woningen die er wél zijn eerlijk te verdelen. Bijvoorbeeld eerst te geven aan de mensen die hoge nood hebben of aan mensen die al heel lang wachten op een woning.

Op langere termijn zou de overheid het aanbieden van woningen kunnen stimuleren door aanbieders subsidie te geven op het bouwen van dit soort woningen.
Of zou de overheid mensen die onterecht wonen in deze goedkope woningen (omdat ze genoeg geld verdienen) moeten ‘dwingen’ om te verhuizen.
5

Het consumentensurplus = het bedrag dat de consument minder hoeft te betalen dan hij maximaal wil betalen.
Het bedrag dat de consument maximaal wil betalen (betalingsbereidheid) is gelijk aan de vraaglijn.

De consument hoeft maar € 700 te betalen.
MAAR: er zijn maar 2 miljoen consumenten die een woning hebben – en alleen díe consumenten kunnen een surplus hebben.

We krijgen nu géén driehoek!

maximumprijs2_02