Een budgetlijn geeft de verschillende combinaties van twee bestedingsmogelijkheden bij een bepaald budget.
De lijn geeft aan in welke combinatie van hoeveelheden we die twee producten kunnen kopen met dat bedrag.
Formule budgetlijn:
Y = (P1 x Q1) + (P2 x Q2)
Y = het budget
P = prijs van resp. product 1 en 2
Q = hoeveelheid van resp. product 1 en 2
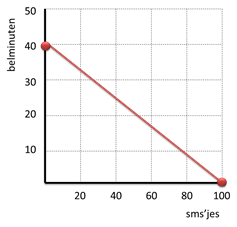
Je hebt een beltegoed van €10,- (budget). Je kunt hiermee bellen voor €0,25 per minuut of sms’en voor €0,10 per bericht.
Met een budgetlijn geef je aan welke combinaties van bellen en sms’en mogelijk zijn voor €10,-
We kunnen eigenlijk al direct de budgetlijn tekenen. Daar is geen formule voor nodig. Het is een rechte lijn en we hoeven alleen maar uit te rekenen hoeveel je kunt kopen wanneer je het hele budget uitgeeft aan één product:
10 = 0,25B + 0,1S
Een prijswijzigingen
Stel dat bellen goedkoper wordt. Voortaan kost een belminuut geen €0,25 maar €0,20.
Je ziet dat de helling van de budgetlijn door de prijsverandering verandert.
Dat kunnen we ook zien (ander hellingsgetal) wanneer we de budgetfunctie opstellen:
Y = (P1 x B) + (P2 x S)
10 = (0,20 x B) + (0,10 x S)
10 = 0,2B + 0,1S
-0,2B = 0,1S – 10
B = -0,5S + 50
Het budget verandert
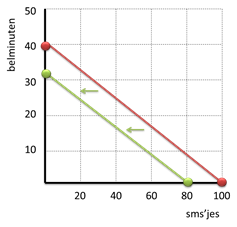
Stel dat je moet bezuinigen. Je kunt voortaan nog maar €8,- besteden en geen €10,-
- Voor €8,- kun je nu nog maar
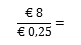 32 minuten bellen, of
32 minuten bellen, of - voor €8,- sms’en. Je kunt dan
 80 sms’jes versturen.
80 sms’jes versturen.
Je ziet dat de budgetlijn evenwijdig verschuift door de verandering van het budget.
Dat kunnen we wederom terug vinden (oude hellingsgetal) in de budgetfunctie:
Y = (P1 x B) + (P2 x S)
8 = (0,25 x B) + (0,10 x S)
8 = 0,25B + 0,1S
-0,25B = 0,1S – 8
B = -0,4S + 32