Uit een onderzoeksrapport, begin 2015:
| De vermogensverschillen in de wereld nemen toe. In 2012 bezat de rijkste 1% van de wereld bijna de helft van het totale vermogen. In 2014 is dat opgelopen naar precies de helft. Als deze ontwikkeling zich doorzet, bezit de rijkste 1% van de wereld in 2016 meer dan de helft van het totale vermogen. |
- Is de vermogensverdeling in ons land in 2014 ten opzichte van 2012 schever geworden?
- Welke maatregelen kunnen genomen worden om een steeds schever wordende vermogensverdeling aan te pakken?
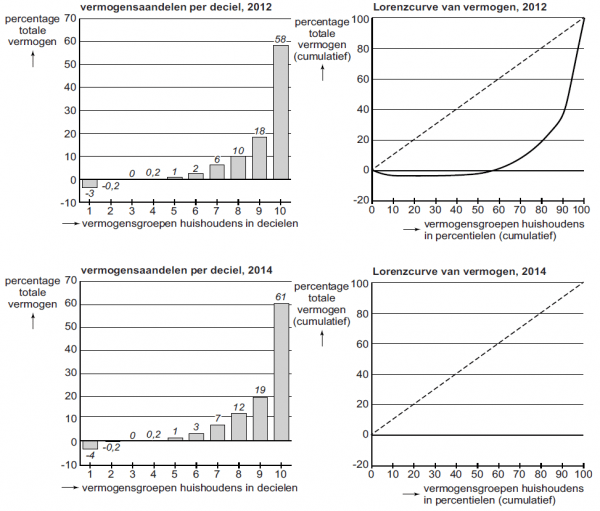
Niels heeft op de site van het Bureau voor Statistiek (BS) statistieken gevonden van de vermogensverdeling in hun land in 2012 en 2014 (bron 1). Hij vraagt zich af: “Hoe kunnen er vermogensgroepen bestaan die 0% of minder van het totale vermogen bezitten, terwijl er binnen die groepen ook huishoudens zijn die spaargeld of een eigen huis hebben, wat volgens het BS ook tot vermogen wordt gerekend?” Eva kan hem dat wel uitleggen.
Gebruik bron 1.
| 1 | Geef namens Eva antwoord op de vraag van Niels. |
De Lorenzcurve van de vermogensverdeling in 2014 heeft Niels niet kunnen vinden. Maar op basis van het staafdiagram van 2014 kan Niels wel een Lorenzcurve van 2014 schetsen.
Gebruik bron 1.
| 2 | Zal de Lorenzcurve van de vermogensverdeling in 2014 een boller of minder bol verloop hebben dan de Lorenzcurve in 2012? Verklaar het antwoord met behulp van de staafdiagrammen. |
Niels en Eva denken dat door middel van een belastingmaatregel de vermogensverschillen kunnen worden aangepakt, met de aanname dat de belasting in mindering wordt gebracht op het vermogen. In hun onderzoek stuiten ze op een nieuwe regeling van de vermogensrendementsheffing die de regering gaat doorvoeren in 2017 (zie bron 3). Niels vergelijkt deze nieuwe regeling met de bestaande regeling in 2014 (zie bron 2) en doet vervolgens twee beweringen:
Gebruik bron 2 en 3.
| 3 | Leg uit dat verhoging van de vrijstelling een nivellerend effect kan hebben op de vermogensverdeling. |
| 4 | Leg uit dat huishoudens met een groot vermogen meer risicospreiding in hun beleggingen kunnen toepassen en zodoende hogere rendementen kunnen behalen. |
Bron 2 regeling vermogensrendementsheffing in 2014
|
Bron 3 regeling vermogensrendementsheffing vanaf 2017
|
||||||||||||||||||||||||||||
Ten slotte willen Niels en Eva uitrekenen of de vermogensverschillen inderdaad afnemen door de nieuwe regeling. Daartoe gaan ze de geplande nieuwe regeling van 2017 vergelijken met de regeling van 2014 voor een huishouden met een vermogen van € 200.000 en een huishouden met een vermogen van € 2.000.000. Ze gaan ervan uit dat tussen 2014 en 2017 geen vermogensgroei heeft plaatsgehad. Eva heeft een tabel gemaakt en de berekeningen voor een huishouden met een vermogen van € 200.000 al ingevuld (zie bron 4).
Gebruik bron 2, 3 en 4.
Bron 4 rekenvoorbeeld regeling vermogensrendementsheffing 2014 en 2017
|
||||||||||||
| 5 |
Zijn op basis van het rekenvoorbeeld de vermogensverschillen na belasting in 2017 ten opzichte van 2014 toegenomen of afgenomen?
|