Opgave 1 – groeifactoren

Rente laat het (nominale) bedrag van je spaarrekening groeien.
De snelste manier om uit te reken hoeveel geld er op je spaarrekening staat na ontvangst van de rente, is met behulp van de groeifactor.

Als je € 1.000 op je spaarrekening hebt staan en na een jaar 5% rente erbij krijgt, heb je na een jaar € 1000 × 1,05 = € 1050.
De groeifactor is 1,05.

1

Bepaal in onderstaande gevallen de groeifactor als het spaargeld 1 jaar op je spaarrekening staat:

  rente groeifactor
a 3% …
b 2,8% …
c 15% …
d 0,5% …
e 100% …
f 0,15% …
g 400% …

 
2

Bepaal in onderstaande gevallen de groeifactor van je spaargeld:

  rente aantal jaren groeifactor
a 3% 4 …
b 5% 20 …
c 0,8% 14 …
d 120% 8 …

 
3

Bepaal in onderstaande gevallen de groeifactor van je spaargeld:

  rente periode groeifactor
a 2,5% 3½ jaar …
b 6% 5 jaar en 8 maanden …
c 1,5% 250 dagen …
d 30% 4 jaar en 5 weken …

 

1
  rente groeifactor
a 3% 1,03
b 2,8% 1,028
c 15% 1,15
d 0,5% 1,005
e 100% 2
f 0,15% 1,15
g 400% 5

 
2
  rente aantal jaren groeifactor
a 3% 4 1,03 4
b 5% 20 1,05 20
c 0,8% 14 1,008 14
d 120% 8 2,2 8

 
3
  rente periode groeifactor
a 2,5% 3½ jaar 1,025 3,5
b 6% 5 jaar en 8 maanden 1,06 5 8/12
c 1,5% 250 dagen 1,015 250/365
d 30% 4 jaar en 5 weken 1,3 4 5/52

 

Opgave 2 – groeifactoren toepassen

4

Charlotte heeft op 1.1.2015 € 2.750 op haar spaarrekening.
De bank geeft een vaste rente van 0,7% per jaar.

⇒ Hoeveel staat er op 1.1.2017 op de spaarrekening van Charlotte?
5

Jan en Jantiene krijgen op 1.1.2017 hun eerste kindje: Kareltje.
Op zijn geboortedag opent zijn opa een spaarrekening, waarop hij € 8.000 stort.
Het geld zal tot zijn 18e verjaardag vast staan tegen een rente van 2,4%. Dan mag Kareltje het geld opnemen. Bijvoorbeeld voor zijn studie.

⇒ Hoeveel geld krijgt Kareltje op zijn 18e verjaardag tot zijn beschikking?
6

Simon opent op 1.1.2016 een spaarrekening. Hij zet er € 1.500 op.
De bank geeft een vaste rente van 1,75%.

⇒ Wat is de waarde van zijn spaarrekening op 1.5.2018?
(Als hij de rekening zou opheffen op die datum.)
7

Martine heeft op 1.1.2010 een spaarrekening geopend. Zij kreeg toen een erfenis van € 15.840. Het hele bedrag heeft zij op de spaarrekening gezet.
De bank geeft op deze spaarrekening 3,25% rente.

In juli 2019 wil zij een wereldreis gaan maken.
Ze zal op 1 juni 2019 daarom de spaarrekening opheffen.

⇒ Hoeveel geld kan zij op 1 juni 2019 afhalen van haar spaarrekening?

4

€ 2.750 × 1,007 2 = € 2.788,63
5

€ 8.000 × 1,024 18 = € 12.259,96
6

€ 1.500 × 1,0175 2 4/12 = € 1.561,97
7

€ 15.840 × 1,0325 9 5/12 = € 21.406,87

Opgave 3 – met een tijdlijn

Wanneer er tussentijds iets verandert, kun je niet meer alleen maar met het groeipercentage de som oplossen. Zo kan de rente op een bepaald moment veranderen, maar het is ook mogelijk dat iemand tussentijds geld opneemt/stort op de spaarrekening.
Het maken van een tijdlijn in dan handig om de periode te splitsen in verschillende groeifactoren.

8

Femke heeft op 1 januari 2014 € 12.000 op een spaarrekening gestort, tegen 4% rente per jaar.
Op 1 januari 2016 neemt zij € 3.000 op. Tenslotte beëindigt zij op 1 september 2017 de rekening en neemt al het overige geld met rente op.

⇒ Hoeveel euro kan zij op 1 sept. 2017 opnemen?
9

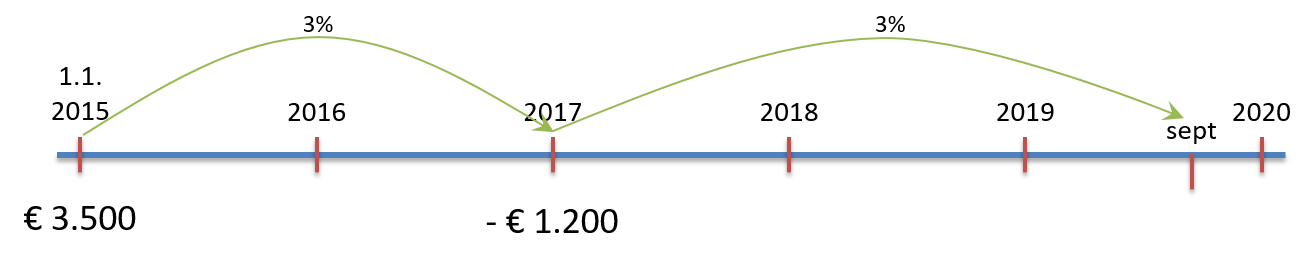
Melvin leent op 1 jan. 2015 € 3.500 tegen 3% rente.
De rente wordt jaarlijks bij zijn schuld opgeteld.

Op 1 jan. 2017 lost hij € 1.200 af van zijn schuld.

Op 1 sept. 2019 wil hij zijn hele schuld in 1× afbetalen.
⇒ Hoeveel moet hij op 1 sept. 2019 betalen om van zijn schuld af te zijn?
10

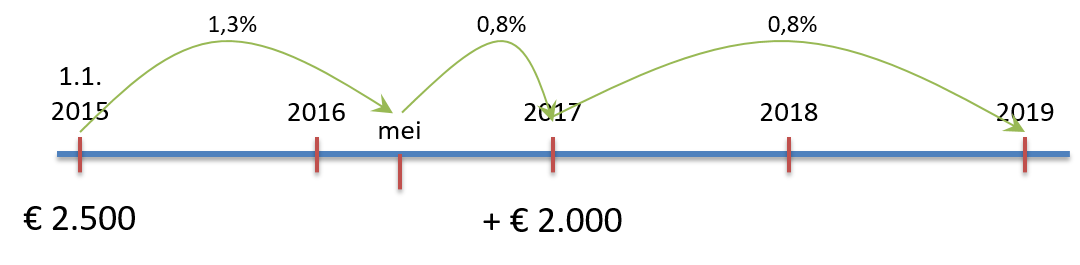
Menno opent een spaarrekening op 1.1.2015. Op dat moment is de spaarrente 1,3%. Hij stort bij het openen € 2.500. 

Op 31.5.2016 verlaagt de bank de spaarrente naar 0,8%.
En op 1.1.2017 stort Menno nog eens € 2.000.

⇒ Hoeveel zal er op 1.1.2019 op de spaarrekening staan als er verder niets meer verandert?

8

De € 12.000 staat er 2 jaar op.
Saldo 1.1.2016: € 12.000 × 1,04 2 = € 12.979,20
Na de opname van € 3.000 staat er dus nog € 9.979,20 op.

Deze € 9.979,20 staat er nog 1 jaar en 8 maanden op.
Saldo 1 sept. 2017: € 9.979,20 × 1,04 1 8/12 = € 10.653,31
9

Na 2 jaar is de schuld van € 3.500 opgelopen tot: € 3.500 × 1,03 2 = € 3.713,15
Na het aflossen van € 1.200 resteert een schuld van € 2.513,15

Dit bedrag loopt in 2 jaar en 8 maanden op tot: € 2.513,15 × 1,03 2 8/12 = € 2.719,26
10

De eerste € 2.500 staat er 1 jaar en 5 maanden op als de bank de rente aanpast.
Het saldo (incl. rente) is dan € 2.500 × 1,013 1 5/12 = € 2.546,17

Deze € 2.546,17 staat er dan nog 7 maanden op (tot de volgende verandering): € 2.546,17 × 1,008 7/12 = € 2.558,03
Dan stort hij nog € 2.000, waardoor het nieuwe saldo € 4.558,03 wordt.

Na 2 jaar is het saldo van de spaarrekening opgelopen tot: € 4.558,03 × 1,008 2 = € 4.631,25