Rekenen met vergelijkingen komt regelmatig terug bij het vak economie. Het is iets dat je bij wiskunde al gehad hebt, maar dat soms tóch leidt tot problemen bij economie. Oefen goed, zodat het stoeien met vergelijkingen geen struikelblok vormt.
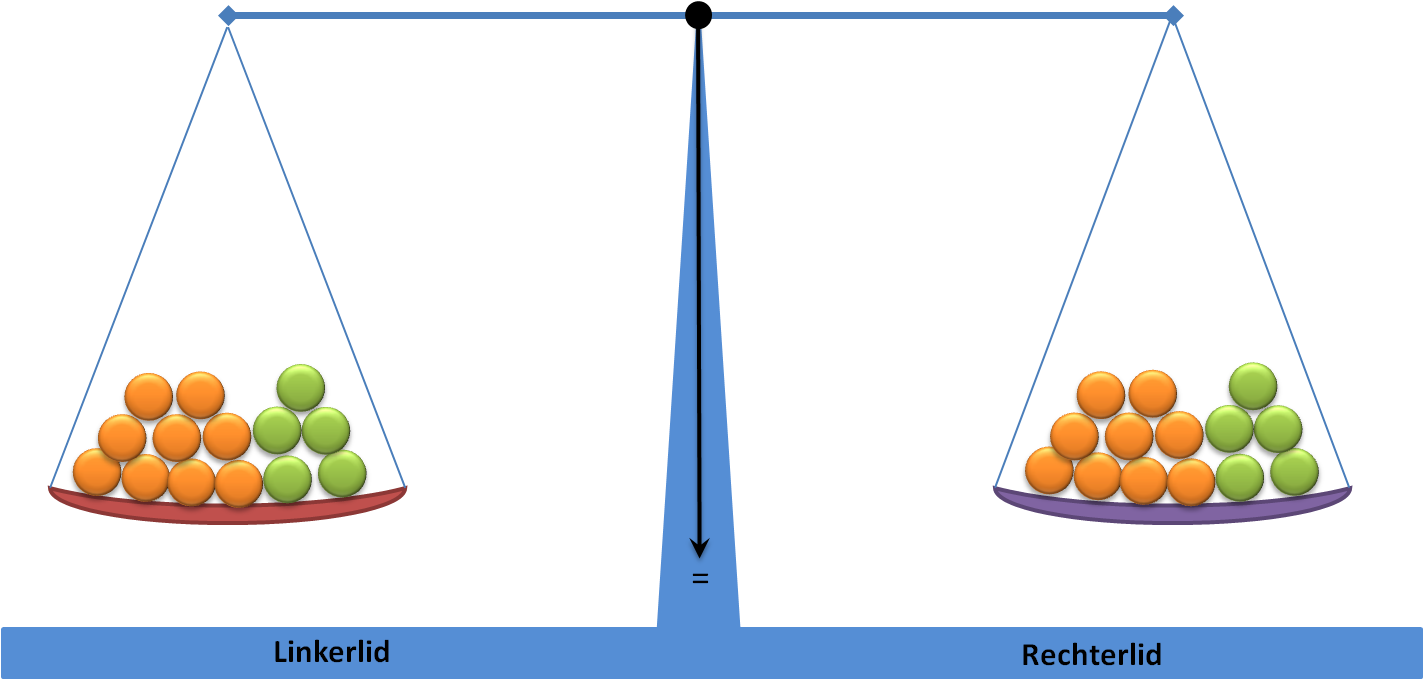
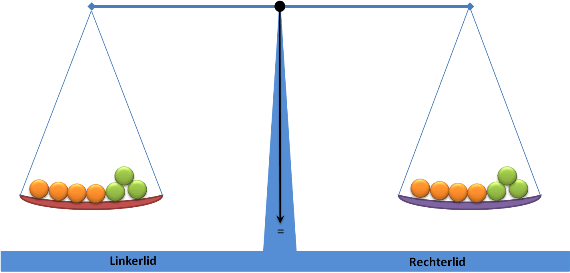
De betekenis van het ‘=’ teken
De weegschaal zal in evenwicht (=) blijven zolang je linker- en rechterlid op dezelfde manier aanpast!
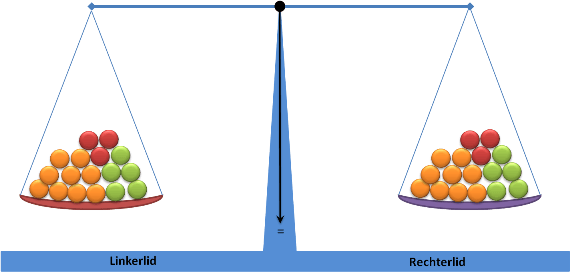
Optellen
De weegschaal blijft in evenwicht zolang we bij de linker- en rechterkant hetzelfde aantal optellen (+3).
| 5x – 3 5x – 3 + 3 5x |
= = = |
10 10 + 3 13 |
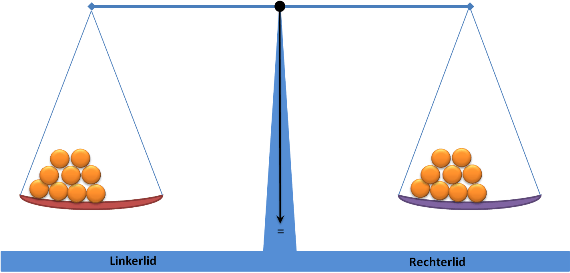
Aftrekken
De weegschaal blijft in evenwicht zolang we aan de linker- en rechterkant hetzelfde aantal weghalen (-5)
| 5x + 5 5x + 5 – 5 5x |
= = = |
14 14 – 5 9 |
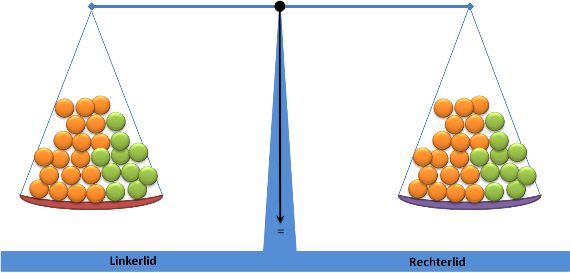
Vermenigvuldigen
De weegschaal blijft in evenwicht zolang we de linker- en rechterkant met hetzelfde aantal vermenigvuldigen
(bijvoorbeeld verdubbelen: x2)
(bijvoorbeeld verdubbelen: x2)
| 0,5y 0,5y x 2 1y |
= = = |
14 14 x 2 28 |
Delen
De weegschaal blijft in evenwicht zolang we de linker- en de rechterkant door dezelfde factor delen (bijvoorbeeld halveren : :2)
| 2x | = | 14 |
| 2x :2 | = | 14 :2 |
| 1x | = | 7 |
Maak nu enkele oefenopgaven over vergelijkingen.
Snijpunt van twee lijnen berekenen
Regelmatig moet in opgaven een snijpunt van twee rechte lijnen worden berekend.
Dat is bijvoorbeeld zo wanneer je de evenwichtsprijs wilt berekenen binnen een marktmodel. Dan moeten vraag en aanbod aan elkaar gelijk zijn: qv = qa
| De weegschaal blijft in evenwicht zolang je links en rechts maar hetzelfde doet, dus wanneer je aan de linkerkant 5x eraf haalt – dan moet je dat rechts ook doen. |
Het marktmodel:
qv = -2p + 10
qa = 4 p – 8
qa = qv
qa = 4 p – 8
qa = qv
| Oplossing | |
|---|---|
| qa = qv | |
| 4p – 8 = -2p + 10 | |
| 4p = -2p + 18 | aan beide kanten +8 |
| 6p = 18 | aan beide kanten +2p |
| p = 3 | aan beide kanten :6 |
Maak nu enkele oefenopgaven over snijpunten berekenen.
Herschrijven van een vergelijking
Soms is het nodig om een vergelijking om te schrijven.
Dat is bijvoorbeeld het geval wanneer we de collectieve vraagfunctie van een monopolist (qv = -2p + 10) willen omzetten in een prijsafzetfunctie voor die monopolist (p = -½q + 5).
| Ook hier gaat het weer om het toepassen van de regel: wat je links doet, moet je rechts ook doen. |
Zet onderstaande vraagfunctie
om in een prijsafzetfunctie:
om in een prijsafzetfunctie:
qv = -2p + 10
| De oplossing | |
|---|---|
| q= -2p + 10 | |
| q + 2p = 10 | aan beide kanten +2p |
| 2p = -q + 10 | aan beide kanten -q |
| p = -½q + 5 | aan beide kanten :2 |
Maak nu enkele oefenopgaven over herschrijven van vergelijkingen.