Om in grafieken waarin bedragen per product staan tóch totaalbedragen aan te kunnen geven, moet je gebieden arceren.
Daarbij kun je gebruik maken van de regel: Lengte x Breedte = Oppervlakte rechthoek.
Aan de hand van een aantal situaties zullen we de regels van het arceren verder bekijken.
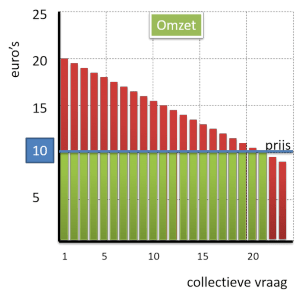
Arceren is het optellen van staafjes per product: omzet
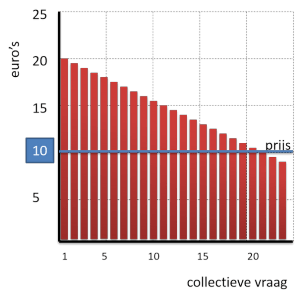
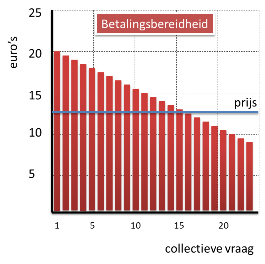
Naarmate de prijs lager wordt, zijn steeds meer mensen bereid het product te kopen.
Bij een prijs van €10 zien we dat 21 personen het product willen kopen.
In de grafiek zijn dat dus 21 staafjes van €10.
Het bedrijf ontvangt dus aan omzet 21 x €10 = €210
Om het totaal uit te rekenen doe je dus 21 (lengte) x €10 (breedte) = €210 (oppervlakte rechthoek).
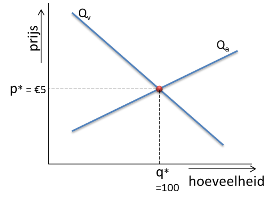
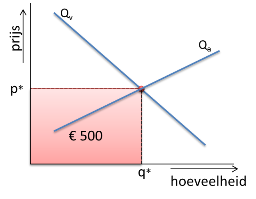
Omzet in marktmodel
In dit model ontstaat een marktevenwicht bij een prijs van €5 en een hoeveelheid van 100 stuks.
Er staan dus eigenlijk 100 staafjes van mensen die €5 betalen.
De marktomzet bedraagt dus: € 5 x 100 stuks = € 500
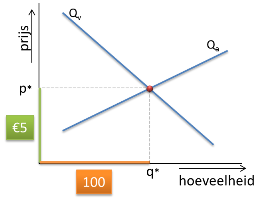
BREEDTE= Het groene lijnstukje geeft de €5,- van de prijs weer in de grafiek.
Oppervlakte = breedte x lengte
Het rode gebied heeft dus een oppervlakte van € 500, de marktomzet.
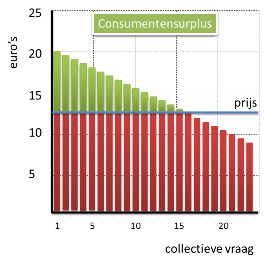
Arceren van een consumentensurplus
Het product kost €12,50
Het consumentensurplus geeft aan hoeveel je minder hoeft te betalen dan je maximaal bereid bent om te betalen.
Omdat de eerste consument bereid is om €20 te betalen, heeft hij een surplus van €7,50
De volgende consument is bereid om €19 te betalen. Deze heeft daarom een surplus van €6,50
enz, enz.
De staafjes die het surplus aangeven worden dus steeds korter.
Het totale consumentensurplus is de optelling van deze staafjes.
De optelling van de (onzichtbare) staafjes vormt de driehoek die het consumentensurplus weer geeft.
De oppervlakte zou je kunnen uitrekenen door: ½ x basis x hoogte.
(uitrekenen valt buiten de examenstof van de havo!)
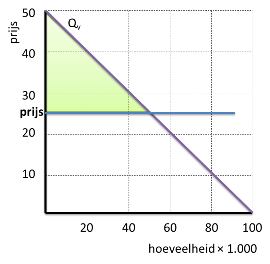
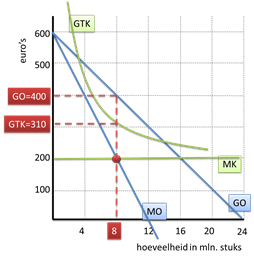
Maximale totale winst bij een monopolist
Wanneer een monopolist maximale totale winst wil halen, moet hij de productie-omvang kiezen waar geldt: MO=MK.
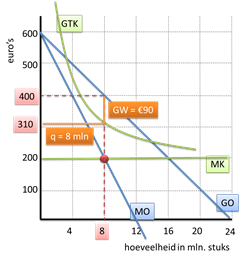
In dit geval zal hij dus kiezen voor een productie-omvang van 8 mln. stuks.
Vervolgens kunnen we op de GO-lijn aflezen dat de prijs(GO) bij 8 mln. stuks €400 is.
Aflezen van de GTK-lijn leert dat bij 8 mln. stuks de GTK €310 bedragen.
Er wordt dus per product €90 winst gemaakt.
Dat zijn dus 8 miljoen staafjes van €90….
Oftewel:
(LENGTE = Q =) 8 mln. stuks en die (BREEDTE = GO-GTK =) € 90 winst per product (GW) opleveren.
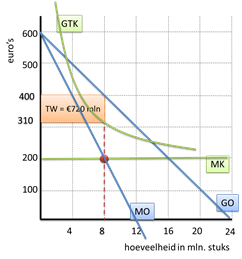
Oppervlakte = breedte x lengte
Het gearceerde gebied heeft dus een oppervlakte van € 720 mln. – de (maximale) totale winst.
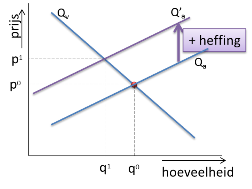
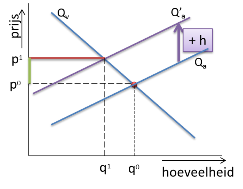
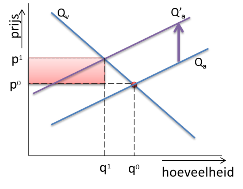
Heffingen
De verschuiving naar boven is gelijk aan het bedrag van de heffing.
Hoeveel gaan de consumenten nu aan extra belasting (heffing) betalen?
LENGTE = rode lijnstuk = q1
BREEDTE = groene lijnstuk = prijsstijging voor de consument