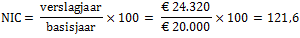|
jaar
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
|
CPI
|
93,6
|
100,0
|
103,2
|
106,0
|
108,4
|
112,5
|
| 2 |
Bereken de procentuele verandering van de prijzen in 2009 (ten opzichte van 2008). |
| 3 |
Bereken de procentuele verandering van de prijzen in de periode 2005 – 2010. [2 decimalen]
|
| 4 |
Bereken de nieuwe reeks met indexcijfers indien 2008 het nieuwe basisjaar wordt.
|
Van de consumentenprijzen is gegeven dat:
CPI2008 = 145
CPI2000 = 120
|
5
|
Met hoeveel procent is het algemene prijspeil in deze periode veranderd? [1 decimaal]
|
Iemand verdient in 2005 een nominaal inkomen van € 40.000. In 2010 neemt dit inkomen toe tot € 45.000
Verder is gegeven, dat de prijzen in 2010 t.o.v. 2005 met 9,7% zijn gestegen.
|
6
|
Met hoeveel procent is het reëel besteedbaar inkomen in 2010 verandert t.o.v. 2005? [1 decimaal]
|
Het CPI stijgt van 110 tot 135.
| 7 |
Hoeveel procent verandert door deze prijsstijging de koopkracht van het geld? [1 decimaal] |
Iemand leent in 2009 € 5.000 van de bank.
Over 5 jaar zal hij dit bedrag in één keer terug betalen. In deze periode zullen de prijzen vermoedelijk met 20% stijgen.
| 8 |
Bereken de koopkracht van deze € 5.000 als dit bedrag (zonder rente) na afloop van de uitleentermijn wordt terugbetaald. |
De bank vraag voor een lening een nominale rente van 5,5%
De inflatie bedraagt 2,2%
| 9 |
Bereken de reële rente die de bank voor de lening vraagt. |
We nemen 2000 als basisjaar.
De lonen stijgen in de periode 2000- 2005 met 12%.
De lonen stijgen in de periode 2005 – 2010 met 5%.
De prijzen stijgen in de periode 2000 – 2005 met 8,5%.
De prijzen dalen in de periode 2005 – 2010 met 1,5%.
Meneer X heeft een vaste uitkering die in het basisjaar € 2000 bedraagt.
Meneer Y heeft een waardevaste uitkering die in het basisjaar € 2000 bedraagt.
Meneer Z heeft een welvaartsvaste uitkering die in het basisjaar € 2000 bedraagt.
| 10 |
Bereken de nominale bedragen die de drie heren in 2005 ontvangen.
|
| 11 |
Bereken met hoeveel procent de reële inkomens van elk van deze drie heren in de periode 2000- 2005 is veranderd. [1 decimaal]
|
| 12 |
Bereken met hoeveel procent het reële inkomen van meneer Z in de hele priode 2000-2010 is veranderd. [1 decimaal]
|
Een producent van computersoftware verhoogt zijn prijs met 5%. Als reactie daarop neemt de omzet met 3% af.
| 13 |
Bereken met hoeveel procent zijn afzet is gedaald. [1 decimaal] |
De productie van een kaasfabrikant neemt met 5% toe. Hiervoor moet hij 2% extra arbeidskracht inhuren.
| 14 |
Bereken de procentuele verandering van de arbeidsproductiviteit [2 decimalen] |
De arbeidsproductiviteit in een productiebedrijf is het afgelopen jaar met 6% gestegen.
De hoeveelheid geproduceerde goederen nam met 4% toe.
| 15 |
Bereken de procentuele verandering van de werkgelegenheid in dit bedrijf. [2 decimalen] |
De werkgelegenheid in een bedrijf stijgt 3 jaar lang jaarlijks met 2%.
De hoeveelheid geproduceerde goederen neemt in deze periode jaarlijks met 4% toe.
| 16 |
Bereken de procentuele verandering van de arbeidsproductiviteit na deze 3 jaren. [1 decimaal] |
Iemand verdient in 2005 € 20.000,-. In 2010 neemt dit inkomen toe tot € 24.320.
Verder is gegeven, dat de prijzen in deze periode met 0,5% daalden.
| 17 |
Met hoeveel procent is het reëel besteedbaar inkomen van deze persoon veranderd? [1 decimaal] |
| 2 |
Gebruik de formule: 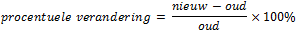
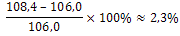
|
| 3 |
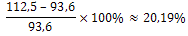
|
| 4 |
Bereken de nieuwe reeks indexcijfers door alle waarden te delen door de waarde van het basisjaar (x 100):
| jaar |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
| CPI |
93,6 |
100,0 |
103,2 |
106,0 |
108,4 |
112,5 |
| |
|
|
|
basisjaar |
|
|
| CPI nieuw |
88,3 |
94,3 |
97,4 |
100 |
102,3 |
106,1 |
|
| 5 |
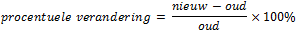
Antwoord: 20,8%
|
| 6 |
Een verandering in het reëel besteedbaar inkomen bereken je met de formule: 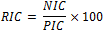
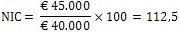
PIC = 109,7
Dus: 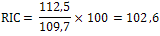 . Het reële inkomen is dus met 2,6% gestegen. . Het reële inkomen is dus met 2,6% gestegen.
|
| 7 |
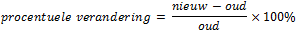
Antwoord: 22,7%
|
| 8 |
Methode 1
Stel dat een product €1,- kost. Dan kan hij nu met het geleende bedrag 5.000 producten kopen.
Over 5 jaar kost het product €1,20 (+20%). Dan kun je met € 5.000 nog maar 4.167 producten kopen.
De koopkracht (het aantal producten dat je kunt kopen) is dus met 16,7% afgenomen.
Methode 2
Je kunt ook gewoon gebruik maken van de formule 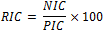
Het nominale bedrag blijft gelijk (NIC=100) en de prijzen stijgen met 20% (PIC=120). Daaruit volgt dat RIC = 83,3 (daling van 16,7%)
|
| 9 |
Ook hier kun je gewoon gebruik maken van de formule 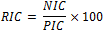
De nominale rente is 5,5% (NIC=105,5) en de prijzen stijgen met 2,2% (PIC=102,2).
Daaruit volgt dat RIC = 103,2 ⇒ een reële rente van 3,2%
|
| 10 |
Meneer X
Vast bedrag, dus € 2000,-
Meneer Y
Waardevast, dus bedrag wordt aangepast aan de prijsstijging: € 2.000 x 1,085 = € 2.170,-
Meneer Z
Welvaartsvast, dus bedrag wordt aangepast aan gemiddelde stijging lonen (welvaart): € 2.000 x 1,12 = € 2.240
|
| 11 |
Om het reële inkomen uit te rekenen gebruiken we de formule: 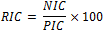
PIC is voor alle heren hetzelfde: 108,5
Meneer X
Vast bedrag, dus NIC = 100 ⇒ RIC = 92,2 ⇒ het reële inkomen (koopkracht) neemt met 7,8% af.
Meneer Y
Waardevast wil zeggen dat de koopkracht van de uitkering constant gehouden wordt door de uitkering met hetzelfde percentage te verhogen als de prijzen. We hoeven dus niet eens te rekenen om te weten dat RIC = 100 (reële inkomen constant).
Dus: NIC = 108,5 ⇒ RIC = 100
Meneer Z
NIC = 112 ⇒ RIC = 103,2 ⇒ het reële inkomen is met 3,2% gestegen.
|
| 12 |
NIC = 100 • 1,12 • 1,05 = 117,6
PIC = 100 • 1,085 • 0,985 = 106,87
RIC = 110,0 ⇒ het reële inkomen is over de gehele periode met zo’n 10% gestegen.
|
| 13 |
Ook hier gaat het om procentuele veranderingen van waarde, prijs en aantal producten.
Ook hier kunnen we dus gebruik maken van de formule; 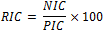
waarbij:
- omzet = NIC = 97 ;
- prijs = PIC = 105 ;
- aantal producten = RIC ⇒ 92,4 ⇒ de afzet daalt met 7,6%
|
| 14 |
Met ‘gewone getallen’ zou je de arbeidsproductiviteit als volgt uitrekenen: 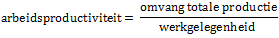
Elke berekening die je met gewone getallen zou doen, kun je ook doen met indexcijfers om de procentuele verandering te berekenen. Dus:
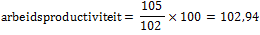 ⇒ de arbeidsproductiviteit steeg met 2,94% ⇒ de arbeidsproductiviteit steeg met 2,94%
|
| 15 |
Ook hier geldt weer:
hoe zou je de werkgelegenheid berekenen met ‘gewone getallen’? ⇒ 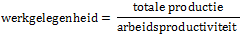
Voer daarna die berekening uit met indexcijfers en je weet de procentuele verandering:
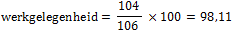 ⇒ de werkgelegenheid nam af met 1,89% ⇒ de werkgelegenheid nam af met 1,89%
|
| 16 |
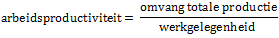
Voer deze berekening uit met indexcijfers.
Werkgelegenheid: (1,02)3 = 1,0612 ⇒ indexcijfer = 106,12
Omvang productie: (1,04)3 = 1,1249 ⇒ indexcijfer = 112,49
Daaruit volgt dat de arbeidsproductiviteit zo’n 6% is gestegen in deze drie jaren.
|
| 17 |
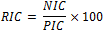
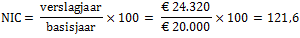
PIC = 99,5
RIC = 122,2 ⇒ het reële inkomen nam met 22,2% toe.
|

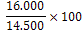
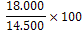
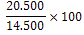
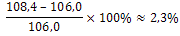
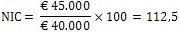
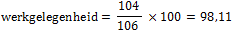 ⇒ de werkgelegenheid nam af met 1,89%
⇒ de werkgelegenheid nam af met 1,89%